摘要：医学图像增强处理中需要很好地解决细节增强与噪声抑制的矛盾。本文提出一种基于模糊逻辑的多尺度医学图像细节增强算法（FLBMEM），根据图像局部特征设计混合滤波器去除脉冲噪声和非脉冲噪声，对不同尺度细节的子带图像进行增强时，根据中心像素与邻域像素的相容性自适应计算非线性细节增益函数，最后各子带图像重建后得到细节增强的图像。试验表明，（FLBMEM）算法增强细节的同时能够有效抑制噪声，能够方便的应用于医学图像处理系统中。
关键词：放射图像；图像增强；多尺度分解；模糊逻辑

1  引 言
   医学图像中经常含有一些重要的低对比度细节，影响医生的诊断。恰当的图像增强处理技术可以提高细节的清晰度，因此图像增强在医学图像应用领域有重要的作用。
   一个标准的图像增强处理方法是反锐化掩模算法(LUM)，将图像分解为高频和低频子带，将高频部分放大后加到原来的图像上，得到细节增强的图像。但这种方法对噪声非常敏感，对含噪声的图像处理会导致噪声放大，反而使图像质量降低。为了提高反锐化掩模算法的性能，后来有学者提出了多种改进算法，如[2][3]采用高阶多项式滤波器产生非线性反锐化掩模算法的高频子带。[4]对这些方法在自然图像的处理效果作了对比，指出这类方法对于高频增强系数非常敏感。另外这些方法有一个明显的缺点是没有考虑图像中间尺寸的结构信息。
   多尺度分解能考察信号在不同频带的结构细节信息，有利于对所需要的结构信息的增强以及噪声的抑制。图像处理中采用的多尺度分解方法主要有小波分解和Laplace金字塔分解，[5]对这两种多尺度分解在医学图像增强中的效果作了对比，指出快速小波变换在医学放射图像增强中可能引入一些伪影。这对于医学图像处理是不恰当的，[6]提出了一种在Laplace多尺度分解基础上的医学图像增强算法，在增强边缘信息的同时有比较好的噪声抑制能力，但是文中的算法需要确定多个参数，如计算每一层的子带增益系数时，有6个参数需要设置，这在实际应用中带来很多不便。为了在增强医学图像细节的同时克服上述缺点，本文提出了一种新的多尺度抗噪增强算法FLBMEM。本文内容安排如下：第二部分介绍算法的总体思路；第三部分和第四部分是混合滤波器与细节增益系数的计算，第五部分给出实验结果分析，最后一部分进行总结。

2  算法描述
FLBMEM算法包括四个步骤：
1) 采用混合滤波器去除原始图像噪声。
2) Laplace金字塔分解。
3) 计算子带增益系数，子带增益系数与细节图像相乘得到增强的细节图像。
4) 重构过程得到增强后的图像。

图 1多尺度图像增强算法示意图
Fig1 Flow chart of FLBMEM

3  混合滤波器
  为了在第一步处理中有效去除噪声，同时避免图像造成模糊，我们设计了基于模糊逻辑规则的混合滤波器。中值滤波对脉冲噪声有很好的滤除效果，均值滤波对非脉冲噪声比较有效，但是图像如果没有受到噪声污染，这两种滤波器都会对图像造成模糊。脉冲噪声的特点是幅值较大，与周围像素有明显的差异，尤其是在平坦区域，严重影响图像视觉质量。非脉冲噪声与周围像素的差异但不如脉冲噪声明显。我们可以根据图像像素点的局部特征判断中心像素点是否被噪声污染，污染噪声的种类，并按照下面的规则采取滤波措施。
规则1：当前像素是脉冲噪声，用中值滤波。
规则2：当前像素被非脉冲噪声污染，用均值滤波。
规则3：当前像素没有噪声污染，保持不变。

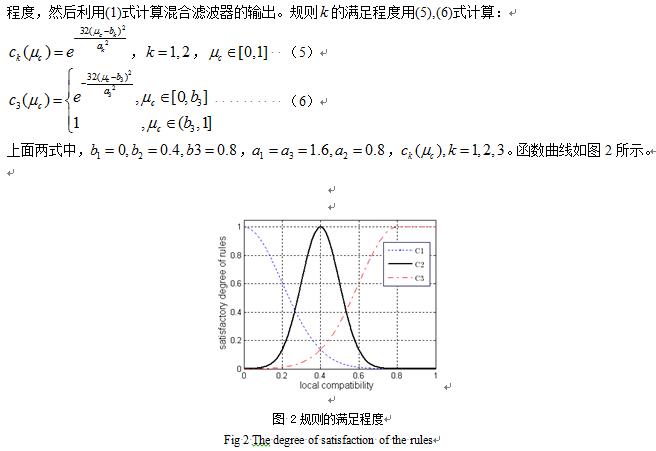
4　子带增益系数

5  实验结果及分析

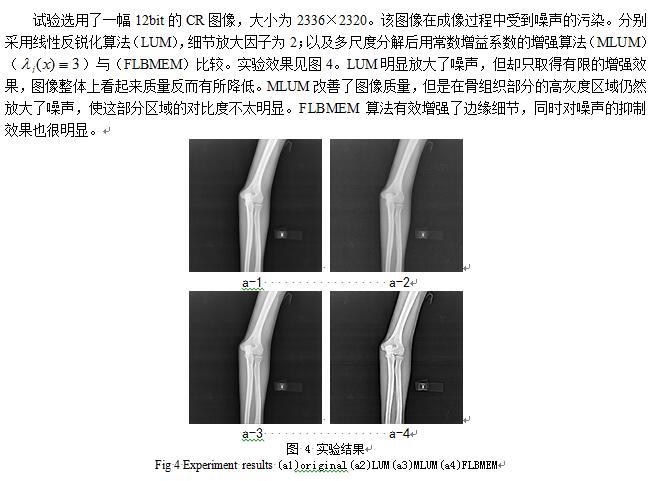
   图5给出了原图及应用上述三种方法(LUM,MLUM, FLBMEM)增强后的直方图，原图的灰度分布主要集中在一个有限的区间(gray scale levels compact in limited region)三种增强算法处理后都将原图像的直方图作了扩展，LUM算法增强后图像的直方图与原图的直方图差别最大，FMLUM增强后图像的直方图与原图像直方图最为相近。
   我们计算图像细节区域的局部方差（detail variance, DV）和背景区域的局部方差(background variance, BV)来客观评价增强算法的效果[6]，BV越大，表示噪声越大，DV越大，表示图像中可见细节就越多。

   由表1可以看出FLBMEM有显著的噪声抑制效果，虽然LUM的DV是最高的，但由于噪声的过度放大，图像的细节信息增强效果并不明显。FLBMEM的DV值虽然比MLUM稍低，但其BV值只有原图BV值的两倍，不到MLUM的BV值的1/4，使MLUM算法增强的图像有更好的视觉效果。
5  结　论
   本文提出了一种基于模糊逻辑的多尺度医学图像锐化增强算法（FLBMEM），试验表明，从视觉质量上和客观评价指标上，本文提出的方法对医学放射图像的细节有很好的增强效果，而且算法使用简单，便于在实际系统中应用。

参 考 文 献

[1] LEE Y H,PARK S Y.“A Study of Convex Concave Edges and Edge-enhancing operators based on the Laplacian”[J]. IEEE Transactions on Circuits and Systems, pp.940-946, 1990,37(7):
[2] G. Ramponi, N. Stroble, S. K. Mitram and T. Yu,“ Nonlinear Unsharp masking methods for imagecontrast enhancement,” J. Electron. Image, Vol.5, pp. 353-366, July 1996.
[3] A. Polesel, G. Ramponi, and V.J. Mathews “Image Enhancement via Adaptive unsharp　masking,” IEEE trans. On image proc. Vol. 9,No. 3, March 2000
[4] Sabine Dippel, Martin Stahl, Rafael Wiemker,and Thomas blaffert “Multiscale Contrast Enhancement for Radiographies: Laplacian Pyramid Versus Fast Wavelet Transform”IEEE trans. On Medical imaging proc. Vol.21.No.4, April 2002
[5] M.A.Badamchizadeh,A.Aghagolzadeh,“Comparative Study of Unsharp Masking Methods for Image Enhancement”,ICIG 2004
[6] 张利平，何金其，黄廉卿，“多尺度抗噪反锐化掩模的医学影像增强算法”，光电工程，第31卷，第10期，2004年10月
[7] Youngsik Chio and Raghu Krishnapuram, “A Robust Approach to Image Enhancement Based on Fuzzy Logic”, IEEE trans. On image processing. Vol.6. No.6. June 1997 p808~p825