摘  要：几何攻击破坏了水印检测器和水印信号的同步性，致使水印检测失败，所以寻求抵抗几何攻击的数字水印算法具有重要意义。本文提出了一种基于Krawtchouk矩和小波变换的抵抗几何攻击的内容认证水印算法。该方法首先对图像进行一次小波分解，然后计算其低频成分的Krawtchouk低阶矩不变量来构建水印。水印提取过程简单，只需计算所得图像的几个低阶Krawtchouk矩不变量。文中给出了实验结果，并与Alghoniemy提出的基于几何矩不变量的数字水印算法进行了比较，结果表明，该方法简单、有效，对旋转、缩放、剪切、组合攻击等几何攻击以及JPEG压缩攻击具有更高的稳健性。

   关键词：数字水印；几何攻击；Krawtchouk矩；小波变换

1引　言

   随着通信、计算机网络技术的飞速发展，多媒体信息的高速传输处理和存储已成为现实。越来越多信息媒体的传输和发布都是通过网络以数字的形式进行。但是数字化的媒体在网上很容易被截获、复制、篡改、盗版和侵权。针对这一问题，国际上提出了一种全新的信息安全与版权保护技术，即数字图像水印技术。它是将鉴别信息以某种编码形式通过数字调制技术嵌入到原始图像中，使得已调制的图像与原始图像在外观上不可区分，而利用后检测手段来认证图像原宿的合法性。但是，像旋转、缩放、剪切等几何操作会因破坏水印检测与嵌入的同步性而导致检测的失效。

   矩函数在图像分析中具有广泛的应用，数字水印技术是其应用领域之一。张力等提出了一种基于Tchebichef矩的数字水印方法[1]，该方法利用Tchebichef 矩估计水印图像所经受的几何攻击参数，并在水印检测之前对水印图像进行恢复，重新获得水印的检测过程和嵌入过程的同步，以便正确地检测水印，但该方法计算量大。Hu把一般的几何矩和代数不变量相结合得到七个几何矩不变量，这些矩不变量在图像旋转、平移、尺度变换下保持不变。2004年Alghoniemy提出了基于该几何矩不变量的数字水印算法[2]。随着图像处理研究的深入，引入了许多新的矩函数，Krawtchouk矩便是其中性能很好的一种[3]。本文提出了基于Krawtchouk矩和小波变换的数字水印算法，首先对图像进行一次小波分解，然后计算其低频成分的Krawtchouk低阶矩不变量来构建水印。该方法水印提取过程简单，只需计算所得图像的几个低阶Krawtchouk矩不变量。文中给出了实验结果，并与基于几何矩不变量的数字水印算法进行了比较。

2Krawtchouk矩和小波变换

2.1小波理论

  小波分析是从傅立叶分析发展出来的一种新的时间频率分析方法，由于它的多尺度分析特征，又被称为时间尺度分析方法。小波变换在时域和频域同时具有良好的局部化性质，而且在小波中的伸缩率与计算机视觉和人眼视觉特征相吻合。1988年Mallat 将小波变换理论用于信号处理,提出了多尺度分析的概念，给出了将图像分解为不同频率通道的算法及其重构算法[4]。

  一个图像信号X的离散小波变换(DWT)可以看作是分别对二维信号的列和行进行高通和低通滤波，相当于一个四通道滤波运算，可以得到二维信号在子带、、和上的变换系数，根据需要可以对子带继续进行分解，直到达到所需要的级数为止。而最低频系数系数绝对值较大，变化范围大，占据了原始图像的绝大部分的能量[5]。

基于小波变换的以上特性，我们可以对图像进行小波变换使得图像能量进一步集中，提取变换后图像的近似分量，在此基础上构建Krawtchouk矩不变量，从而使算法更加具有稳健性。在本文第4部分，进行了仿真并给出了实验结果，进一步证明了改方法的有效性。

2.2 Krawtchouk多项式和Krawtchouk矩

  Krawtchouk矩是基于经典的离散Krawtchouk多项式提出的一组新的正交矩。利用图像的Krawtchouk矩可以很好地恢复出原始图像[3]。而且在不管有无噪声干扰的情况下都要比Zernike、Legendre、Tchebichef等矩性能更好。

  Krawtchouk矩的核函数是由一系列的Krawtchouk多项式组成的。n阶的Krawtchouk多项式定义如下：

2.3 Krawtchouk矩不变量

   Krawtchouk矩不变量定义如下，它是不随图像的平移、旋转、尺度变化而变化的矩特征量。

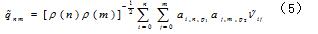
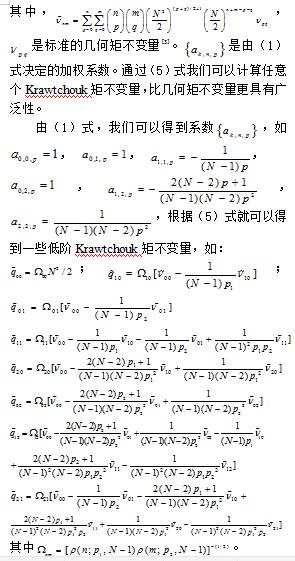
   为了检验Krawtchouk矩不变量对各种攻击的稳健性，应用StirMark攻击软件对大小为256×256的图像“girl”进行攻击，检测它的Krawtchouk矩不变量。为了减少攻击后图像Krawtchouk矩不变量的波动，更加简洁地说明问题，对不变量进行一些处理，即。

   表1给出了图像“girl”经过各种攻击后的结果。由于与图像内容无关，所以选择剩下的7个不变量进行实验。由表1可以看到，在几何攻击和常见攻击条件下，7个Krawtchouk矩不变量变化都不大，尤其是低阶矩不变量，变化量基本上都小于0.02，所以可以利用它的不变性对数字图像进行保护。由以上的推导过程可以看到，矩本身是关于图像内容的函数，所以不同的图像具有不同的Krawtchouk矩不变量值。所以表1中的Krawtchouk矩不变量的值只反映了图像“girl”的内容。

3　基于Krawtchouk矩和小波变换不变量的水印算法

   本节将提出一种基于小波变换和Krawtchouk矩不变量的抵抗几何攻击操作的水印算法。首先对图像进行一维小波分解，提取近似分量，然后提取Krawtchouk矩不变量计算其偏差来检验水印是否存在。进行小波分解后使图像能量进一步集中，因此这种方法比直接提取Krawtchouk矩不变量更具有稳健性。由表1可以看到这七个低阶Krawtchouk矩不变量对几何攻击具有稳健性，所以关于这七个不变量的的函数也是几乎不变的。因此，我们根据关于不变量的函数和一个参考值来检测水印的存在。

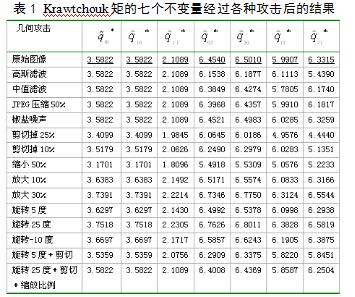
   关于不变量的任何函数，线性的、非线性的。N为一常量，是由实验确定的容忍度，取值很小。

   嵌入水印图像实际上就是原始图像加上一个扰动图像，即                   （7）

   其中为扰动图像，定义为： 。为关于I的映射函数，一般选为log函数。为比例系数，调节以使。

3.2解码过程

   为了确定接收的图像是否可信，我们只需验证（6）式是否成立。实际上是验证偏差E，即是否在容忍范围内。当接收到图像的偏差时，认为该图像是可信的，否则不可信。

   通过解码过程我们可以知道：第一，该解码过程为盲提取过程不需要原始图像，我们只需知道常量N和预先规定的容忍度；第二，通过（6）式对接收到的图像进行检测，只是回答了是或否，可信或不可信的问题，是一个认证的过程，所以该方法的水印容量只有1bit。

3.3参数设定

   由（6）式可知，N是一个标准参量，是判断接收图像是否可信的一个标准，它为附近的任何一个值，在的调节下使其等于。决定了偏离N的容忍程度，它由容忍的攻击强度决定。越大，容忍的攻击强度越大，反之则越小，一般在实验中取为0.2～0.3。

函数的确定：它可以是关于不变量的任何函数。为了安全起见，函数可以作为密钥保存起来，以增加该算法的安全性。一般，被设计成个七不变量的加权平均值。由表1我们可以看到，随着矩的阶数增加，不变量的波动性变大，所以可以让阶数较大的不变量的权值较小，低阶的权值较大，这样以使偏差减小，系统更加稳健。如：

（8）                                      

几点说明：

容量：以上提出的水印算法只是一个证明系统，它只回答了是或否，因此它是一个容量为1bit的水印系统；

稳健性：该方法对几何攻击具有较强的稳健性。因为所用的Krawtchouk矩不变量对几何攻击是不变的；

安全性：的设置、函数的权值设置都可作为密钥，提高了该算法的安全性；

盲检测：我们可以看到，该算法的提取过程不需要原始图像。在解码过程中，我们只要知道预先设置的N、和的权值就可以完成检测；

计算复杂度：本算法的编码和解码过程都非常简单。主要就是计算偏差E，判断它是否在容忍度的范围内。

4 实验结果

   经过小波分解后，图像的能量更加集中，提取的图像不变量更加稳健。图1为旋转不同角度后，进行小波变换和不进行变换的偏差，图2为不同缩放比例下的偏差。点划线是没有进行小波变换的结果，实线是进行变换后的结果。由图1和图2可以看到，进行小波变换后，图像不变量的偏差E明显减少。所以先进行一次小波变换再提取不变量的算法更具有稳健性。

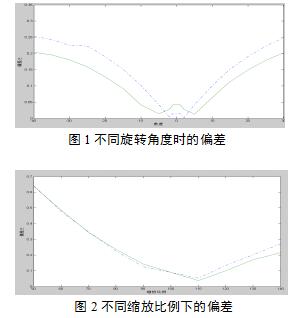
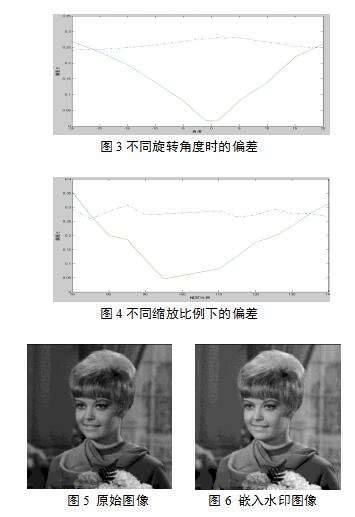
   将本文算法与基于传统的七个几何矩不变量的数字水印算法[2]进行比较。图3、图4分别给出了在不同旋转角度和缩放比例情况下的不变量偏差。点划线是几何矩的结果，实线是Krawtchouk矩的结果。由图可以看出，当旋转角度从－20度到＋20度，缩放比例从75％到135％变化时，基于Krawtchouk矩不变量的算法的偏差比基于几何矩不变量的算法偏差要小得很多，所以本文算法具有更强的抗攻击能力。

   在水印检测的实验中我们所用图像是大小为256×256的灰度图像“girl”，如图5所示。＝5.28，根据（7）式得到嵌入水印图像，如图6所示。选择为各不变量的加权平均值，如（8）式所示。对嵌入水印图像施加软件StirMark产生的攻击，结果如表2所示。经过实验确定=0.2，N＝3.71。

   由表2可以看出，本文算法对滤波、JPEG压缩、剪切、缩放、旋转等单一的几何攻击具有较强的稳健性。旋转角度可以从-15度到10度，缩放比例可以从85％到125％。而且对组合攻击也具有较强的稳健性，旋转剪切组合攻击中，旋转角度可以达到20度，旋转剪切缩放比例组合攻击中，旋转角度可以到达25度。

5 结　论

  几何攻击对水印算法具有致命性的影响，将使水印算法彻底失败。本文提出的基于小波变换和Krawtchouk矩不变量的数字水印算法，除了对压缩、滤波等常见攻击具有稳健性以外，对旋转、缩放、剪切和组合攻击等几何攻击也具有较好的稳健性。实验表明该算法是可靠的。该算法解码过程不需要原始图像，且编码和解码过程简单，但是水印的嵌入量只有1bit。所以如何增大嵌入水印信息量是今后要研究的一个重要方向。

参考文献

[1] 张力,韦岗,张基宏, Tchebichef矩在图像数字水印技术中的应用, 通信学报,2003, 24(9):10-18

[2] M. Alghoniemy, H. Tewfik, “Geometric Invariance in Image Watermarking”, IEEE Trans. Image Processing, 2004, 13(2):145-153  

[3] P. Yap, P. Raveendran, and S. Ong, Image analysis by Krawtchouk moments, IEEE Transactions on Image Processing, 2003, 12(11):1367-1377

[4] Stokes L F, Chodorow M, Shaw H J, All-single-mode fiber resonator[J], 1982, 7(6):.288-290

[5] 台莉春,高珍,张志浩,基于小波变换的数字水印最佳嵌入位置的研究, 微型电脑应用, 2005, 21(4):11-14