摘  要：在矢量地图中隐含水印信息，地图数据的质量往往由于水印的嵌入而受到影响。可逆水印技术(又称无损数据隐藏)具有完整恢复载体数据的能力，因而更加适用于矢量地图。本文基于差值扩大的思想，提出了一种应用于矢量地图的无损数据隐藏算法。算法根据矢量地图对数据精度的特殊要求提出了相应的水印嵌入条件，并通过修改地图中相邻顶点坐标间的差值来嵌入水印信息。水印的提取过程不仅能够得到隐藏信息，而且能够准确无误的恢复原始地图数据。实验结果表明算法具有较高的信息载荷(约0.58 bit/vertex)，其应用前景包括矢量地图数据的篡改鉴别、元数据格式兼容以及基于矢量地图的隐藏通信。

   摘  要：矢量地图；无损数据隐藏；差值扩大；信息载荷

1 引　言

   随着地理信息系统的广泛应用，数字矢量地图在分发和使用过程中存在的诸如版权保护、篡改鉴别等数据安全问题日益凸显出来。数字水印技术被引入到矢量地图数据中，成为解决此类问题的重要辅助手段[1-4]。但是，水印数据的嵌入不可避免的会给原始地图数据带来扰动，在一定程度上降低了地图数据的质量。可逆水印技术又称为无损数据隐藏，是指能够完整恢复原始载体数据的水印算法。该技术主要应用于原始载体数据不容篡改的场合，如医学影像和用于法庭证据的数据。由于矢量地图的应用环境比较严格，通常希望避免对原始地图数据的任何改动，因此可逆水印技术对于矢量地图数据具有很强的适用性。目前可逆水印技术的研究主要集中在栅格图象领域，主要的方法包括利用可逆模加[5]、无损压缩[6]、改变直方图[7,8]和差值扩大[9]来实现算法的可逆性，针对二维矢量数据的可逆算法研究则较少受到关注。M. Voigt等人通过改变原始矢量地图数据的整数DCT系数来隐含水印信息[10]，这也是目前公开发表的关于二维矢量图形可逆水印算法的仅有的一篇文献。该算法存在的主要缺陷是水印嵌入对含水印地图数据造成的扰动过大。国内也有人进行矢量地图水印算法的研究工作[11-15]，但尚未见到有关可逆算法的讨论。

   差值扩大法[9]是由J. Tian提出的一种用于栅格图象的可逆水印算法。本文借鉴该算法的实现思想，提出了一种矢量地图空间域无损数据隐藏算法。矢量地图数据与栅格图象数据在应用环境上的区别决定了在这两类数据之中嵌入水印信息必须遵循不同的嵌入原则。栅格图象水印需要保证图象的视觉质量，而矢量地图水印则关注数据精度。本文根据矢量地图对数据精度的严格要求提出了采用差值扩大法嵌入水印的条件，通过对地图中满足嵌入精度条件的相邻顶点的坐标差值进行移位操作，在不损失原始信息的情况下为水印数据提供额外的存储空间。算法的实质是利用了地图临近顶点坐标数据具有较强相关性的特点。当隐藏的水印信息被提取出来之后，原始地图数据能够得到无损的恢复。

2 差值扩大技术

   差值扩大技术由J.Tian提出，用于在数字图象中实现无损数据隐藏，其基本思想可以归结为：针对具有较强相关性的原始载体数据中的相邻数据点和(原始数据均为整数)，首先用一组可逆变换来分别计算二者的差值和整数均值，即

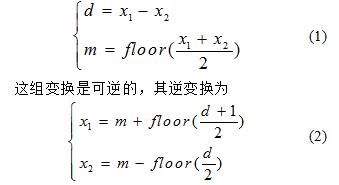
   其中表示向下取整。载体数据的相关性意味着大多数情况下和的取值比较接近，因此其差值通常比较小。在一定的误差范围内，通过将值扩大为原来的倍(即左移位)，即可为待隐藏的数据提供比特的冗余空间。将带有隐藏数据的差值记为，结合原先的整数均值，含水印数据可以通过逆变换[公式(2)]得到。差值扩大算法用于无损数据隐藏具有两个主要的优点：首先，由于值本身较小，因此水印嵌入引入的误差较小；另外，由逆变换可知，每个差值上引入的误差()将由两个数据点和共同承担，因此每个数据点所承受的误差比较均匀。

3 矢量地图的无损数据隐藏方案

   由前文分析可见，差值扩大技术在本质上是利用了原始数据的相关性来为隐藏数据提供存储空间。大多数自然图像数据具有强相关性的特点，即临近像素通常具有相近的灰度值。而矢量地图元素(多边曲线和多边形)是由大量密集的顶点按照特定的顺序排列而成的，地图数据就是这些顶点的二维坐标序列。在同一地图元素中，顶点的密集性使得大多数相邻顶点的位置十分接近，坐标数据间的差值也很小。地图坐标数据体现出的这种强相关性使得差值扩大技术能够应用于二维矢量地图的无损数据隐藏。

3.1 顶点分组变换与嵌入精度条件判断

1)顶点分组变换

   一幅原始地图必然由点、线段、多边曲线和多边形四种类型的元素构成。点元素只包含一个顶点，因此不能用作数据隐藏。对于其他类型的每一个元素，首先进行顶点分组。以一个元素为例，假设该元素所包含的顶点表示为，将所有顶点按照先后顺序，每相邻两点作为一组，则该元素的顶点被划分为。对原始地图中除点元素以外的所有元素都采用上述方法进行分组，则原始地图中绝大多数相邻顶点都两两组合为“顶点对”。假设其总数为，则其中任意一组可以表示为：

   其中和为构成该组的两个顶点，而和分别是这两点的二维坐标。接下来对每组中的两个顶点，分别计算其横、纵坐标的差值和整数均值，即

   要在原始地图的横坐标(纵坐标)中隐藏信息，只需要将差值扩大技术应用到差值序列中。即对中符合条件的数据向左移位，并将空出来的数据位用于存放待隐藏的信息。

2)嵌入精度条件

   通常矢量地图数据都有各自的精度误差容限(记为)，当地图坐标数据受到的扰动低于时，不会影响地图的可用性。因此，水印嵌入所引入的坐标误差通常也应该小于。在这个限制下，并不是所有的坐标差值和都适合进行移位操作的，必须满足一定的嵌入精度条件。本文仅考虑差值扩大2倍(即左移一位)的情况，假设当前需要将水印数据位嵌入到“顶点对”的横坐标中，则数据嵌入后对应的差值变为：

 经过无损压缩后的数据。在水印提取阶段，当隐含的水印信息被提取出来之后，为进一步恢复原始地图数据，必须知道哪些“顶点对”在水印嵌入时采用了差值扩大法，因此标志数据需要成为隐含水印信息的一部分，以供数据恢复阶段使用。

 水印嵌入时，差值序列中对应为1的元素将用差值扩大的方式来隐含水印数据，而对应为0的元素将采用直接替换最不显著位(LSB)的方式来存储水印信息。因此，为保证算法的可逆性，这些原始的LSB数据必须保存下来以供数据恢复时使用。就是差值序列中所有对应为0的元素的LSB组成的数据。和一样，它经过无损压缩后，也作为水印数据的一部分。

 有效信息载荷。根据水印系统所需完成的功能，可以是原始地图数据的数字摘要(用于篡改鉴别)，或者是地图元数据(用于地图格式兼容)，也可以是用户需要传输的信息(作为一种隐藏通信方式)。

 一些额外的控制数据，用于将前述三类数据合理的组织起来以构成完整的水印数据。

   如果原始地图划分的“顶点对”的总数为，则最终生成的水印数据的长度也为，记为。算法的实际有效信息载荷为：

其中表示二进制长度。

   是由水印数据直接替换的最低位得到的，因此为得到，需要将的最低位还原成相应的原始值，式中为中的索引。得到原始差值序列后，结合整数均值序列，即可通过式(2)完全恢复原始地图数据。因此，本算法为无损的数据隐藏算法。

4 实验结果

   将本算法应用于多种不同特征的矢量地图，都取得了较好的效果。图1是实验所用原始地图的一种。该图为我国河流分布图，比例尺为1:400万，总共包含顶点数目为252000个，地图坐标数据为精确到小数点后六位的小数。由于本算法适用于整数，因此实验前需先将所有数据乘以转换成整数坐标。实验地图的精度误差容限为Km。为增加有效的信息载荷，本文在地图横、纵坐标中均隐藏数据，尽管含水印地图的部分顶点的误差超过了误差容限，但由于本算法能够完全恢复原始地图数据，因此并不影响地图的使用价值。实验中的有效隐藏信息包含三个部分，分别是原始地图的MD5哈希值(128 bits)、地图元数据(10998 bits)、和一幅的灰度图象(135424 bits，见图2)，这三部分数据分别用于原始地图的篡改检测、元数据格式兼容和隐藏通信。

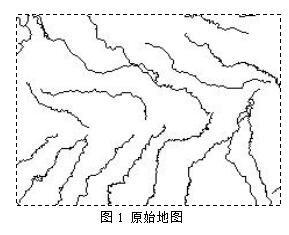
   图3为包含隐藏信息的地图，可以看到算法没有对地图引入过大的扰动。图4为提取的水印图象，图5为恢复后的原始地图，MD5哈希值的比较可以证明该图与原始地图完全相同。算法的实际信息载荷为146550 bits，平均约为0.58 bit/vertex。

5 结 论

本文提出了一种应用于矢量地图数据的无损数据隐藏算法。由于矢量地图的应用环境比较严格，不允许随意改动数据，因此数据隐藏的可逆性对于矢量地图水印具有十分重要的意义。基于差值扩大的思想，本算法利用地图相邻顶点坐标的相关性，将隐藏信息嵌入到地图数据的横、纵坐标中。算法引入的扰动比较小，而且能够完全恢复原始地图数据。算法的有效信息载荷约为0.58 bit/vertex，通常能够容纳原始地图的数字摘要、元数据、以及一定长度的秘密信息，从而能够实现对原始地图数据的篡改鉴别、元数据格式兼容以及基于矢量地图的隐藏通信。算法的缺陷是地图顶点的扰动方向没有考虑原始地图的形状特征，因此在充分放大的地图中，这些扰动使地图具有不自然的外形特征。使算法具有更好的形状保持特性和更高的有效信息载荷是我们正在进行的工作。

参 考 文 献

[1]  Ohbuchi R, Ueda H, Endoh S. Robust watermarking of vector digital maps[C]. in Proc of IEEE International Conference on Multimedia and Expo(ICME ’02), Lausanne, Switzerland, Augest 26–29, 2002, vol 1, pp 577–580.

[2]  Voigt M, Busch C. Feature-ba sed watermarking of 2d-vector data[C]. in Proceedings of SPIE, Security and watermarking of Multimedia Content, vol 5020, Santa Clara, USA, 2003, pp 359–366.

[3]  Nikolaidis N, Pitas I, Solachidis V. Fourier desc riptors watermarking of vector graphics images[C]. in Proceedings of International Conference on Image Processing, Vancouver, BC, Canada, September 10–13, 2000, vol 3, pp 9–12.

[4]  Li Y Y, Xu L P. A blind watermarking of vector graphics images[C]. in Proceedings of Fifth International Conference on Computational Intelligence and Multimedia Applications, (ICCIMA 2003), Xi’an, P.R. China, Sept.27–30 2003, pp 424-429.

[5]  Honsinger C W, Jones P, Rabbani M, et al. Lossless recovery of an original image containing em bedded data[P]. US patent applicat, Docket No 77 102/E-D, 1999.

[6]  Fridrich J, Goljan J, Du R. Invertible authentication[C]. Proceedings of SPIE 2001, Security and Watermarking of Multimedia Content, San Jose, CA, Jan 2001, 3971: 197-208.

[7]  Ni Z, Shi Y Q, Ansari N, et al. Reversible data hiding[C]. Proceedings of International Symposium on Circuits and Systems (ISCAS 2003), Bangkok, Thailand, May, 2003, (2): 912-915.

[8]  Leest A, Veen M, Bruekers F. Reversible image watermarking[C]. IEEE Proceedings of ICIP’03, September 2003, (2):731-734.

[9]  Tian J. Reversible watermarking by difference expansion[C]. Proceedings of Workshop on Multimedia and Security, Dec 2002, 19-22.

[10]  Voigt M, Yang B, Busch C. Reversible watermarking of 2d-vector data[C]. in Proceedings of the 2004 multimedia and security workshop on Multimedia and security, Sept 2004, 160-165

[11]  周旭, 毕笃彦. 基于中国剩余定理的GIS数字水印算法[J]. 中国图形图像学报, 2004, 9(5):611-615

[12]  王勋, 林海, 鲍虎军. 一种鲁棒的矢量地图数字水印算法[J]. 计算机辅助设计与图形学学报, 2004, 16(10): 1377-1381.

[13]  李媛媛, 许录平. 用于矢量地图版权保护的数字水印[J]. 西安电子科技大学学报（自然科学版）, 2004, 31(5): 719-723

[14]  胡云, 伍宏涛, 张涵钰, 等. 矢量数据中水印系统的设计与实现[J]. 计算机工程与应用, 2004, 40(21): 28-30

[15]  张海涛, 李兆平, 孙乐兵. 地理信息水印系统的开发[J]. 测绘通报, 2004, 5: 42-44