图象图形学在木材纹理特征检测中的应用
于海鹏  刘一星  刘镇波
（东北林业大学生物质材料科学与技术教育部重点实验室，哈尔滨  150040）

摘  要： 基于图象图形学方法，实现了对木材纹理灰度特征的分析，并应用计算机自动检测出木材纹理形状、角度、周期长度、线宽度和间距等特征量值。试验结果证实，BWMORPH函数最适于木材类中弱纹理形状轮廓的检测，可以生成新的纹理骨骼线图象；对纹理骨骼线图象进行Radon变换后，可绘制纹理角度的二维曲线图，纹理曲线图所反映的木材纹理角度朝向规律与人们日常印象相吻合；通过将纹理图象二值化后再横向扫描的方式，能够得到纹理的峰-谷周期图，从中能够准确计算出纹理的周期长度，对应于木材的生长轮宽度，并可进一步求出纹理的线宽度和纹理的间距，分别对应木材的早、晚材宽度。
关键词： 图象图形学；木材；纹理；特征检测
Abstract: Assisted by image and graphics technology, it analyzed textural gray characters of wood, and detcted features of textural shape, directionality, period run-length, textural width, and textural spacing with computer. Results has proved, BWMORPH was best suitable function for detecting such weak texture shape as wood, and could generated a skeletal texture image. After Radon transform on the skeletal texture image, a two dimensional curve plot was drawn to represent textural directionality of wood. By scanning pixel value across binary textural region, it could obtained apex vs vale periodic plot, and calculated textural period run-length, textural width, textural spacing which were respectively corresponding with growth-ring width, latewood width and earlywood width.
key words:  Image and graphics; Wood; texture; Feature detecting

    对于纹理型事物而言，纹理的形状、角度、周期性、纹理宽度及间距等都是定义其类属的关键参数。木材因其分子结构和被切削方式不同，表现在不同切面呈现出独特的纹理模式，可以解释这是由生长轮、早、晚材宽度的规律性但非均匀变化所引起的。木材纹理特征与木材自身的结构属性息息相关，因此对木材纹理特征量的针对性检测是必要的。但国内外应用图象图形学方法来探测木材纹理特征量的研究报告还十分有限。
    本文将选择典型的木材径向、弦向切面纹理图象（如图1所示），应用图象图形学手段来尝试提取它们的纹理特征信息。
 
      
(a) 径向纹理                 (b) 弦向纹理
图1  典型的木材径向、弦向纹理图象
Fig.1 Typical radial and tangential textural images of wood
1  木材纹理灰度的变动特征及规律
1.1 木材纹理灰度的周期特性
    有规则的灰度变化才形成纹理，纹理是灰度分布的周期性；即便灰度变化是随机的，它也具有一定的统计特性，所以对纹理的分析也需要从纹理的灰度变动特性进行。
    对典型的木材径切面纹理图象，沿垂直于纹理方向横向扫描得到图象宽度范围内的纹理灰度变化数据，如图2所示。可以看出，木材纹理灰度基本呈周期性变化，每一个周期由若干个灰度像素点构成，周期长度和周期内灰度最大变动幅值基本相等。
 
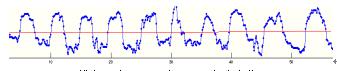
图2  横向扫描纹理区域所得的灰度变化图
Fig.2  Gray fluctuant plot by across scanning texture region
1.2 木材纹理灰度的自相似特性
    木材纹理灰度的自相似特性可由相邻像素点之间的散点图来分析（图3）。散点图是根据相邻两像素的灰度值，以前一灰度值为横坐标，后一灰度值为纵坐标而描点绘图。散点图中各散点以45°角直线为轴心分布，长轴反映灰度值的变化范围，短轴反映灰度值的变化幅度大小。

  
    分析图3可知，数据点基本都围绕在45°直线附近分布，呈线性关系，长轴宽度很大，短轴宽度较小，说明在很大的灰度变化范围内，相邻灰度点之间的相关性仍很密切，不随灰度的绝对值变化而改变，这说明了木材纹理灰度间的自相似特性。
1.3 木材纹理灰度差值的变动特征
1.3.1 纹理灰度差值的散点图分析
    每相邻两像素灰度值之间的差值可反映纹理细微变动的幅度，相应的数据可形成纹理灰度差值系列，如图4所示。分析图4可知，灰度差值以“0”为水平基线而上下波动，说明灰度的改变并不定向；整体上多数数据点紧贴基线或在基线附近，说明产生这些数据点的相邻两像素间的灰度变动很小；灰度差值的极大值一般呈周期性出现，且基本规律为正向差值极大值和负向差值极大值相间隔出现。
 
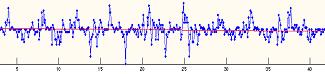
图4  纹理灰度差值变化图
Fig.4  Gray-difference fluctuant plot of adjacent values
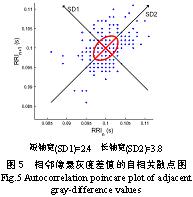
    纹理灰度差值数据的自相关散点图见图5。分析图5可知，每相邻两数据点的分布虽比较密集，但并不紧贴45°直线附近，说明灰度间差值变化的整个范围内，木材纹理灰度的变动幅值在一定范围内呈随机变化，相邻灰度间差值点之间总体具有一定规律，但相关性不很密切。此外，从长、短轴的宽度来看，灰度间差值的变动幅度不大，即木材纹理灰度呈一个小幅度的随机变动，故不会引起视觉的敏感和刺激。

1.3.2 纹理灰度差值的频谱分析
    利用纹理灰度差值数据做出自回归模型功率谱图和快速傅里叶变换功率谱图（如图6），并分析它们所表达的木材纹理灰度的频谱特征。

(a) 自回归模型功率谱
 
(b) 快速傅里叶变换功率谱
图6  木材纹理灰度差值的功率谱图
Fig.6  Spectrum of gray-difference values of wood texture
    从图6中可以看出，在极低频（0~0.05Hz）和低频（0.05~0.15Hz）范围内，灰度差值的功率谱密度峰值均较低，而在高频（0.15~0.4Hz）范围却出现了功率谱密度值的明显尖峰；功率谱能量的比值约为（极低频+低频）/高频≈0.29（AR功率谱）或0.16（FFT功率谱），显示灰度变动差值以高频为主，只间或出现灰度的低频跳变，与图4和图5表达的信息相印证。
    综合以上分析结果，可以总结出木材纹理灰度变动的规律为：在一个纹理灰度变动周期内，绝大多数相邻像素间的灰度值具有很高的自相似性，灰度值的变动一般呈现高频度、小幅值、随机性的特点；而处在相邻周期衔接处的像素点间自相似性一般不密切，灰度差的变动往往呈现低频度、大幅值、有规律的特点，此处往往对应视觉上纹理灰度的跳跃部位；在整个图象区域内，若干个纹理周期的特点表现为总体相似，但不完全相同。
2  木材纹理形状与纹理角度的检测
    形状是物体的一种属性，但实际上定义物体的形状确实非常困难。虽然当前并没有被认可的统一的形状描述方法学，但定位于物体边界一阶导数的显著变化常常会产生适当的信息。
    在描述图象视觉属性的众多特征中，方向性也值得被作为一个与众不同的属性来对待。图象图形学强调，方向性是判定一幅图象与另一幅图象是否相似的一个关键的定义，并且基于这样的假设，将图象内容在二维空间内所表现出来的角度谱作为图象内容和分类的一个特征尺度。
    木材纹理方向的定量检测仍是尚未被完全解决的问题之一。据理论分析，Radon变换能够从嘈杂背景中提取出直线系列（也可认为是曲线），从而将一幅二维的图象转换成为一个线性参数域，二维图象中的每一条直线都会在线性参数域中的对应角度位置上产生一个顶点，因而在检测纹理方向方面具有极大的潜力[1~2]。
2.1 木材纹理形状的检测
    以MATLAB6.5为辅助工具，使用“UIGETFILE”和“IMREAD”函数打开各种图象格式的木材纹理图象文件，读取像素灰度值并形成二维矩阵（灰度图象）或三维矩阵（彩色图象）。通常，彩色图象被转变成灰度图象或二值图象，达到降维的目的，适用的Matlab函数为“RGB2GRAY”和“IM2BW”。
    尝试应用基于数学形态学原理[3~4]的“IMCONTOUR”、“EDGE”、“BWPERIM”和“BWMORPH”四个Matlab函数来探测纹理形状。IMCONTOUR 函数能够勾勒出输入灰度图象的形态轮廓图。EDGE函数能够将一幅灰度图象中被认为是边界的像素点值标以“1”，其它非边界区域的像素点值标为“0”，从而将灰度图象转变为一幅具有相同尺寸的二值图象。BWPERIM函数能够起到探测灰度图象内部物体周边缘的作用，返回一幅相同尺寸的二值图象。BWMORPH函数通常是对输入图象执行二值形态学的计算，并返回一幅输入图象的纹理形态骨骼线二值图象[5]。
    利用四种函数对木材纹理形状探测的结果显示，IMCONTOUR不能够简洁地描述纹理的外形，产生的纹理边缘线条太多，如图7(a)所示；EDGE函数不能够对弱纹理的图象取得完整的边缘形状，如图7(b)所示，因而它们都不是理想的纹理形状探测函数。相反，基于BWPERIM函数和BWMORPH函数都能够取得简洁而完整的纹理形状二值图象，如图7(c)、图7(d)所示。
  
(a) IMCONTOUR函数变换
  
(b) EDGE函数变换
  
(c) BWPERIM函数变换
  
(d) BWMORPH函数变换
图7  基于不同函数的木材纹理形状的探测
Fig.7  Detection of textural shapes by different functions
2.2 木材纹理线图象的Radon变换
    Radon变换的原理是计算图象矩阵在指定方向上的投影。Radon变换算子将空间域的像素点集 映射到它的投影变换域 ，以 作为直线朝向角度、ρ作为直线距坐标系原点的最短距离。对应于每个角度的强度值都是原图象中沿此角度方向的直线数量的积分。各种角度直线的Radon变换汇织在一起就常常显现为一幅角度-强度图。
    在经Radon变换后的角度-强度图中，经常会发现一些特别明显的交汇点，它们一般对应着高的积分值，显示原图象中存在对应此亮点角度的直线或直线集合。对经BWPERIM函数变换和BWMORPH函数变换得到的二值图象再进行Radon变换，如图8所示，可以看出它们图中的高幅值点的位置和排列都非常相近，差别只是BWPERIM图Radon变换后的亮点数量略多，这显示BWPERIM函数和BWMORPH函数都适合于检测纹理的形状及方向。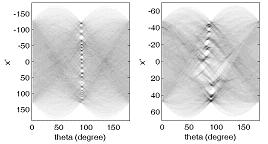
  
(a) BWPERIM图象的Radon变换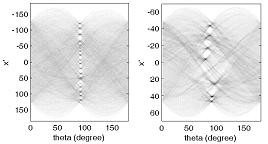
  
(b) BWMORPH图象的Radon变换
图8  BWPERIM图象和BWMORPH图象的Radon变换比较
Fig. 8  Radon transform of BWPERIM and BWMORPH images
2.3 木材纹理角度二维曲线图
    在Radon变换图中，每个高亮点的角度位置坐标都会对应于原图象中的一条或多条较明显的直线。如果这些亮点值能够被在Radon变换结果的矩阵中找到，则原图象的纹理方向就会很清楚了。使用“MAX”函数寻找出Radon变换矩阵中每一个 （角度）列中的最大ρ值，生成 二维曲线图，如图9所示。根据图9，可以发现BWPERIM和BWMORPH图象的Radon检测变换都会对明显纹理的树种具有很好的方向指示作用。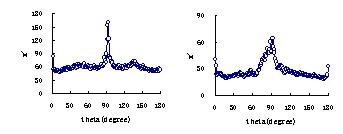
  
(a) BWPERIM图象的Radon变换纹理方向曲线图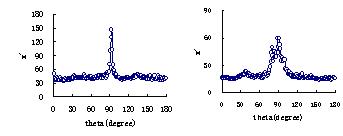
  
(b) BWMORPH图象的Radon变换纹理方向曲线图
图9  BWPERIM图象和BWMORPH图象的纹理方向图
Fig. 9  Textural directionality plot from RT images
    但是对一些纹理程度较弱或者是不呈明显纹理状的树种，例如白桦（Betula platyphylla），它的BWPERIM图象Radon变换纹理方向图和BWMORPH图象的不同，如图10所示。BWPERIM图象的Radon变换纹理方向图中在90°和0°处都有值超过300的高峰，与原图象相比，可认为出现了伪纹理。而从BWMORPH图象的Radon变换纹理方向图中，在0°~180°角度范围上，纹理曲线的变化比较平缓，不存在某个角度上的峰值急剧变化，整条曲线形式显示原图象纹理不呈明显的方向性。基于此，可以认为对于那些弱纹理或不呈纹理状的树种来说，利用BWMORPH函数要比BWPERIM函数提取纹理形状效果好。
  
(a) BWPERIM图象角度图 (b) BWMORPH图象角度图
图10  白桦图象的纹理方向曲线图
Fig. 10  Texture orientation plot of Betula platyphylla
3 木材纹理周期、宽度及间距的检测
3.1 木材纹理周期的灰度变动幅度
    IMPROFILE函数可以计算图象中沿线段经过路径的像度值，因此如果垂直于木材纹理方向画一条线段使之横穿过纹理区域，就会获取线段沿途像素的强度值并生成像素强度对线段距离的二维曲线图。选择在木材图象竖直方向的中段，画一宽度为11像素、长度等于图象宽度的矩形框使之横穿纹理区域，检测矩形框覆盖区域的像素灰度变化情况。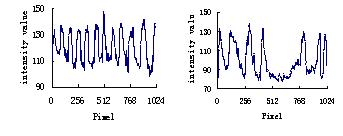
  
图11  IMPROFILE函数检测木材纹理灰度图象的周期变动
Fig.11  Detection of texture alteration by IMPROFILE function
    如图11所示，木材纹理中存在着明显的周期性灰度幅值的变化，并且各纹理周期的灰度强度最大、最小值都基本相当。所以，若相当数量纹理周期内的灰度峰谷强度之差可以被测量出，则纹理周期的灰度变动程度就可得知。例如，图11的平均纹理灰度变动差20.6和30.1。
3.2 木材纹理周期长度检测
    纹理的周期长度可以认为是纹理灰度强度经历一个谷、峰周期变化过程的行程，对应于木材也可认为是一个生长轮的宽度。若对图1直接检测，则会因伪峰的出现而造成周期长度检测结果不准确。改进方法为，首先运用最大方差法对纹理进行二值分割；可以发现，二值图象中纹理图形的界限是清晰而明显的，这就为纹理周期长度的检测提供了可行性。纹理周期长度的检测，也使用到IMPROFILE函数，检测矩形方框覆盖的纹理区域内像素幅值的0、1变化情况，并编程计算出像素值由取0开始、到连续为1结束的长度的出现频度，如图12所示。
     

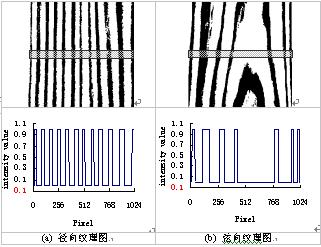
图12  IMPROFILE函数检测木材纹理二值图象的周期变动
Fig. 12  IMPROFILE detection of binary wood images
    对图12的纹理周期长度检测后，统计计算得到的纹理周期长度数据：（1）对径向切面纹理的图12(a)，出现过的纹理周期长度有32、65、79、80、81、82、90、96、100和119共10个值，平均长度值为82.4；（2）对弦向切面纹理的图12(b)，出现过的纹理周期长度有40、56、113、136、138、141和387共7个值，平均长度值为116.8。
3.3 木材纹理宽度及间距检测
    当测量出了纹理周期长度（木材的生长轮宽度）之后，既而又想得知其中究竟有多少是属于早材的宽度，又有多少是属于晚材的宽度呢？即按图象处理常规，如果把一个生长轮的晚材部分当作为纹理线宽度、早材部分当作为纹理间距时，它们各自对应的距离又是多少呢？
    对图12的二值图象扫描数据再作分析，在每一个纹理周期中，测量出像素值连续为“0”和像素值连续为“1”的像点数目，分别对应于一个生长轮内的早材宽度和晚材宽度。
   （1）对径切面纹理图12(a)，其晚材宽度，即连续“1”值的长度数据有20、23、30、31、34、38、45、49，其中出现频数超过一次的有23、30、34，平均值为30.11；晚材的总宽度占整个纹理宽度的37.3%。早材宽度，即连续“0”值的长度数据有13、43、49、51、52、56、59、68、71、76，其中出现频数超过一次的有49，平均值为49.57；早材的总宽度占整个纹理宽度的62.7%。
   （2）对弦切面纹理12(b)，其晚材宽度为19、24、26、28、41、50、69，它们的出现频数均未超过一次，平均值为36.71；晚材的总宽度占整个纹理宽度的25.1%。早材宽度为13、38、68、88、92、115、347，出现频数也均未超过一次，平均值为108.71；早材的总宽度占整个纹理宽度的74.9%。
4  小结
    本文通过实例分析充分说明了图象图形学在木材纹理特征检测中的可应用性，对木材纹理的形状、角度、周期、宽度及间距等重要特征计算机直接检测方法，将对此类纹理事物的定量化分析具有参考价值。

参 考 文 献

[1] Wang Jin-ping. Some Properties of Radon Operator[J]. Acta Scientiarum Naturalium Universitatis NeiMongol, 1999, 30(6): 675~676
[2] Rey M.T., Tunaley J.K.E., Folinsbee J.T., et al. Application of Radon Transform Techniques to Wake Detection in Seas at a SAR Images[J]. IEEE Trans. Geosci. Remote Sensing, 1990, 28(4): 553~560
[3] Serra J.. Introduction to Mathematical Morphology[J]. Computer Vision, Graphics, and Image processing, 1986, 35(3): 283~305
[4] Steinberg S.R.. Grayscale Morphology[J]. Graphics, and Image processing, 1986, 35(3): 333~355
[5] Matlab. MATLAB 6.1 Help Document[M], the MathWorks, Inc., 2001