摘 要：在PCB贴片安装的机器视觉检测中需要通过图像配准拼接来得到整个PCB的图像，传统的图像配准拼接技术由于光照干扰效果不好。用图像的小波分解高频系数去除反映光照渐变的低能量系数后，可以较好地避免光照不均匀的干扰。分别利用小波分解有效垂直高频系数的垂直投影和水平高频系数的水平投影可以快速水平配准和垂直配准，低频部分作拼接的灰度渐变平滑处理。实验结果显示了本算法的鲁棒性、快速和良好拼接效果。
 关键词：图像拼接; 小波变换; 图像配准; 机器视觉; 自动光学检测

1    引   言
    随着电子制造业的印刷电路板（PCB）元件安装采用表面贴片安装技术(SMT)，并且贴片元器件向着越来越小、密度越来越高的方向发展，贴片安装的传统目检已无法完成检测任务，基于机器视觉的自动光学检测（AOI）成为替代其的新技术[1]，高效、可靠的机器视觉自动检测成为电子制造业自动化的一个重要组成部分。为了保证检测精度，图像采集的分辨率要求达到20m/pixel，即1270dpi。这样即使600万像素的CCD也只能达到46cm的视野（FOV），事实上目前AOI的图像采集视野就是在cm数量级[2]。这样检测整个PCB必须借助高精度X-Y移动平台来移动CCD或PCB板，逐帧采集图像，然后分析检测。
    但在最初采集后，需要得到整个PCB板的信息，以确定检测时的采集路线、采集位置、范围，以避免无元件的非检测区的采集和对小元件不必要的分隔[3]。因此必须用逐帧移动采集的图像来进行图像拼接以得到整个PCB的图像。
    关于图像拼接或镶嵌的研究，主要应用在遥感图像采集、虚拟现实等领域。它包括重叠部分的图像配准和接缝处的接缝消除两部分。由于AOI的工程环境，使得传统的图像配准方法应用效果不好。  如图1是两幅待拼接图像，图2是图1中取第二幅图 的重叠部分作模板，在第一幅图中作水平移动互相关处理找匹配位置的结果[4]，

                       
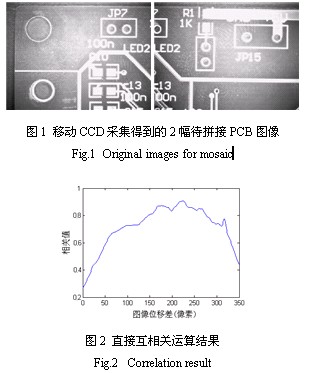
由于光照的影响干扰，在像移311像素点处的互相关峰值基本被噪声掩盖。
    AOI图像拼接的具体工程特点为：（1）因为AOI的放大，光照较弱且不均匀，对采集的图像影响很大，表现为图像中间亮、周围渐暗，两幅拼接图像的重叠配准部分的灰度变化趋势是相反的。（2）AOI各帧图像的旋转误差很小，可以忽略。（3）PCB图像纹理有其特点，可以在拼接的配准时加以利用。（4）AOI对检测速度有实时性要求，所以必须改进算法的复杂度。
     结合AOI检测的工程实际，本文对其图像拼接进行了研究和实验。

2   基于小波分解高频系数的图像配准
2.1   小波分解系数的特性
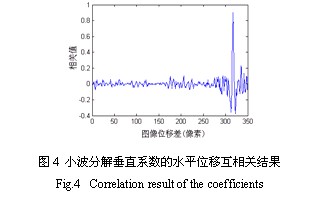
    小波变换具有良好的时频分辨性能。图像配准依据的是图像的轮廓，而小波分解的高频系数正好反映了图像的变化轮廓[5]。Xu等提出了基于小波分解高频系数相关的配准方法[6]，黄铜城等提出了以被嵌入图像的低频部分作背景、结合嵌入图像的高频系数重新合成的消除镶嵌接缝的方法[7]。如图3是图1原始图像的小波分解垂直系数，它反映了图像中水平方向的灰度变化，即图像中物体的垂直轮廓。
                           

    从图3可以看到，光照不均匀虽然还存在，但由于其是渐变，所以其能量和物体的轮廓变化相比数值很小。图4是该小波分解系数的水平互相关结果，峰值尖锐、突出，可以准确找到水平偏差位置。

2.2  基于图像投影的快速配准
     但是在PCB贴片安装机器视觉检测（AOI）的具体工程应用中，贴片生产线对AOI检测速度有实时性要求[2]。而互相关处理的运算量是很大的，MN的模板互相关的计算量为(MN)2次乘运算，这样加上小波变换的时间开销，无法满足检测的时间要求。而小波变换是必要的，因为按1200dpi的图像采集分辨率，一块5050cm的PCB拼接后图像将达到1.6GB[2]，这样的内存消耗显然是无法实现的。而拼接得到的图像，只是为了作检测路径规划[3]，减小分辨率到1/16，即80m/pixel，对于最小的0201元件0.3mm的尺寸在图像上为3个像素，仍然可以检出，可以满足路径规划的需要。所以做2级小波分解，用1级分解后的高频系数求图像拼接配准的偏差位置，低频部分再次分解后拼接。
    由于AOI中的X-Y移动平台精度较高，误差为6-10m，即小于1个像素。这样水平拼接图像配准时可以考虑直接利用图像的垂直投影，将配准图像数据从2维降低到1维，减少配准运算量[8]。垂直拼接图像则利用图像的水平投影。一幅MN图像的垂直和水平投影平均值分别为[4]：
                       
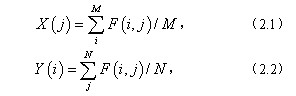
    其中F(i,j)为图像在(i,j)像素点处的灰度值，M为图像行数，N为列数。X(j)为第j列像素的灰度垂直投影，Y(i)为第i行像素的灰度水平投影。
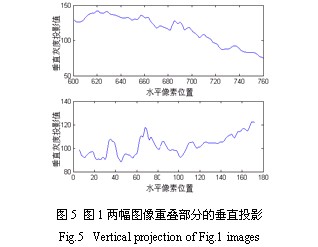
    但是在PCB贴片AOI工程实际中，由于图像放大、光照的干扰，直接作图像灰度投影与直接作互相关运算配准一样，配准精度差，甚至难以配准。如图5为图1两幅原始图像的重叠部分的垂直投影。在左图的690点和右图的68点处应该是相似的峰值处，但受照明噪声干扰变得不明显。并可看出左图灰度逐渐降低、右图灰度逐渐增高的光照变化。结合小波分解高频系数的特点来作投影，则可以得到较好的效果。   

2.3   小波分解高频系数的投影
    对数字图像的2维小波变换可以分解得到低频成分和分别反映图像水平变化、反映垂直变化和反映斜向变化的高频系数4部分，而且4部分不仅具有频域特性，还仍然保持了原图像的位置特性[5]。如图3是图1的小波分解的垂直高频系数，它较好地反映了原图像在垂直方向的轮廓，图4显示了利用其作水平偏差互相关计算的良好结果。为减小计算量，我们用小波分解系数作投影代替2维互相关运算。如图6是图1的两幅图像分别作小波分解后垂直高频系数的垂直投影。
                      
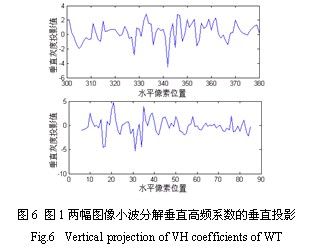
    从图中可以看出两幅图像的相似性，及左图340-350点处的三个峰值在右图30-40点处的对应。已看不出光照的变化，但其渐变干扰仍然存在，表现为低能量的噪声。
2.4  小波分解高频大系数投影的快速配准
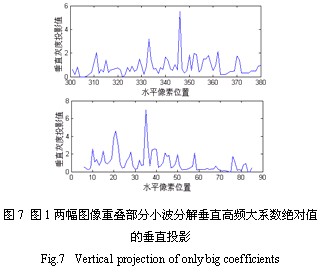
    与基于阈值的小波变换降噪方法类似，在小波分解高频系数中设定阈值，绝对值小于阈值的认为是噪声，取值为零。实际上，在这里的AOI采集的图像中，光照的不均匀表现为渐变，在高频域表现为低能量的系数；而物体轮廓变化明显，表现为高能量大系数。而且这里分解后的高频系数是用于配准，而不用再合成恢复[2]，所以可以去掉低能量的高频小系数。阈值的确定需要根据具体的图像，也可根据具体图像的高频系数最大幅度乘以系数来确定。如图6为图1的图像小波分解后的垂直高频系数，经取阈值为20去除低能量小系数后的垂直投影。
    从图中可以看出，图像小波分解后的高频系数，去除噪声干扰等低能量系数后，剩下的高频小波系数反映了图像的主要轮廓，其中两幅图像重叠部分经处理后相似性很好。由于在AOI的具体工程实际中，偏差相对固定，所以不必再做互相关计算，可以直接在预计的水平偏差位置附近求该垂直高频小波大系数垂直投影的极大值位置，即可快速得到两幅图像的水平偏差。
    同理通过水平高频小波大系数的水平投影极大值的位置，可以得到垂直偏差，从而实现快速配准。如图7为图1两幅图像的小波分解水平大系数的水平投影，可见垂直偏差很小，仅1个像素。 
                       
3  图像接缝的灰度渐变平滑
    待拼接的图像配准后，直接连接会有明显的接缝，在AOI工程实际中由于光照不均匀会更明显。接缝处直接取平均也仍然有接缝痕迹，这些都会对后续的图像分割产生误差。如图8为图1两幅图在接缝重叠处取平均值的拼接效果，可以看到2条明显的接缝痕迹
                          

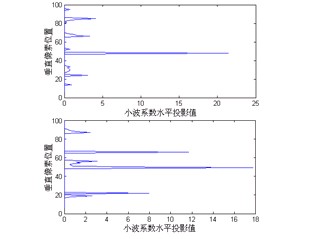
图8    图1 小波分解的水平高频大系数绝对值的水平投影
Fig.8    Horizontal projection of only big coefficients。

    为此可以采取距离灰度渐变的方法[7]，接缝重叠处的灰度随距离的增加，取各图的灰度比例减小来合成[8]：
                           
    F(i,j)为接缝处(i,j)像素点处理后的灰度值，F1、F2为待拼接的两幅图像上对应的像素点的灰度值，xd、yd分别两幅图像的水平偏差和垂直偏差，图1中分别为311和1。md为拼接时接缝重叠部分的宽度。
                          
4  实验和结论
    我们按本方案进行AOI实际图像采集拼接实验。图像采集的光学放大为0.35，CCD为768576像素的1/2”黑白CCD，X-Y移动平台精度为10m。这样视野约为2.51.8cm，采集时每次水平移动2cm，一行采集后垂直移动1.3cm。分别对多块不同大小的电路板进行了图像采集拼接实验。如图7为4幅图像拼接的效果。
 拼接时，先完成各行图像的水平拼接，然后进行行间的垂直拼接。
    分别对86cm、1210cm、2520cm等各种规格、绿、红、蓝、黑、黄等各色基板的PCB进行采 集拼接，结果均快速、准确地配准，拼接接缝平滑，显示了本算法良好的鲁棒性。
                
实验结果表明：本文提出的基于小波分解大系数X-Y方向投影的快速配准拼接方案，不受光照不均匀的干扰，鲁棒性强，速度快，在PCB贴片安装生产自动机器视觉检测的工程实践中有实际应用价值。在其它要求快速图像配准、图像镶嵌拼接的应用领域也可以结合具体实际进行推广应用。

参 考 文 献

 [1] A. Gallegos-Hernandez, F. J. Ruiz-Sanchez, J. R. Villalobos-Cano, "2D automated visual inspection system for the remote quality control of SMD assembly"[J], Proc. of IEEE 28th Annual Conference of the Industrial Electronics Society, vol.3, pp.2219-2224, 2002.
 [2] 罗兵, 章云, SMT质量缺陷和AOI检测方法[J], 电子质量,vol.6, pp.30-32, 2006.
 [3] Hwa-Jung Kim, Tae-Hyoung Park, "A clustering algorithm for path planning of SMT inspection machines"[J], Proc. of the Annual Conf. of the Society of Instrument and Control Engineers, vol.3, pp.2869-2874, 2003.
 [4] W. K. Pratt, 数字图像处理[M], 北京: 机械工业出版社, pp.425-429, 2005.
 [5] I. Daubechies, “The Wavelet Transform, Time-Frequency Localization and Signal Processing”[J], IEEE Trans. on Information Theory, vol.36, pp.961-1005, 1990.
 [6] D. Xu, B. Paul, J. Y. Shi, “Image mosaics based on complex wavelet decomposition”[J], Journal of Software, vol.9, pp.656- 661, 1998.
 [7] 黄铜城，胡运发, 基于多分辨率特征的图像镶嵌技术, 计算机工程, vol.32(7), pp.23-25, 2006.
 [8] 侯舒维，郭宝龙, 一种图像自动拼接的快速算法, 计算机工程, vol.31(15), pp.70-72, 2005.