摘  要:模糊是一种常见的失真现象，其表现是边缘的平滑效应。对边缘扩散邻域的一阶微分求取峰态能反映出图像的清晰程度，提出一种基于边缘峰态的无参考图像清晰度评价。实验结果表明，该方法不依赖图像内容，与图像的清晰程度表现一致，且对噪声不是很敏感。
关键词:清晰度评价；边缘峰态；无参考；模糊

1.引　言
 模糊是一种常见的图像失真现象，在图像获取、传输及处理过程中有许多因素会造成图像模糊，如成像系统的聚焦不良、与景物的相对运动、光的衍射以及图像压缩之后高频丢失等产生的各类模糊。模糊现象严重影响了图像的质量，降低了图像的清晰度，导致图像分析和场景理解的困难。因此，在成像系统的自动聚焦、图像增强及压缩等算法的衡量、流媒体的质量控制等方面，无参考图像的模糊度量或清晰度评价都是很有必要的，大量的研究致力于此[1-8]。
 模糊的一个明显表现为边缘的平滑，导致边缘宽度的增加，因此很多研究都是基于对边缘的分析。文献[1]基于模糊边缘的平滑效应，提出一种在空间域中衡量边缘扩散的方法，该方法具有运算复杂度低，接近实时的优点。针对文献[1]在水平/垂直方向计算边缘扩散，在文献[2]中改进为计算与边缘垂直的梯度方向及反方向上的边缘扩散，但它们都存在对噪声敏感的问题。文献[3]中通过获取边缘梯度幅度信息，以其标准差来表示模糊边缘宽度，结合加权的边缘梯度幅值，使其结果更加稳定。在另一方面，清晰度也是衡量模糊图像质量的一个度量，如在数字成像设备中就经常采用梯度函数、频谱函数、熵函数等对图像的清晰度进行评价[4]，但图像内容的不同对这些方法的影响比较大。在文献[5]中采用改进的边缘锐度算法，也是基于对边缘的分析：灰度变化越激烈，边缘越清晰，图像也越清晰。为了获得锐化指标，一些研究人员利用了边缘的峰态信息[6，7]，不同之处在于[6]中的峰态计算基于边缘区域的8x8块的DCT系数，而文献[7]则在小波域中计算峰态信息。此外，峰态信息也用于图像的盲复原过程中作为复原图像质量的度量[8]。
 在本文中，我们提出一种基于峰态的无参考模糊图像评价的新方法，与前述的不同之处在于我们所采用的峰态定义在空间域中，免去了变换到频域的复杂性。实验表明，该方法不依赖图像内容，与图像的清晰程度表现一致，对噪声不是很敏感。
2  在空域中定义的峰态
   假设场景中有一条尖锐边缘，其一维剖面图如图1所示，对其求导后可得到一阶导数脉冲图，模糊边缘的一阶导数脉冲图则相对扁平，类似于不同核的高斯函数。将一阶导数脉冲值归一化后，我们可以采用峰态来衡量其陡峭程度。

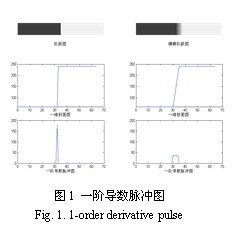
    峰态是描述正态性的一个统计量，定义为标准化的四阶中心矩[8]：

其中，表示随机变量x的均值，表示标准差，E表示数学期望。

    直观上，峰态指频数分布曲线高峰的形态,即反映分布曲线的尖峭程度的测度。总体峰态系数为3时,为正态分布;大于3时,其分布较正态分布的峰尖峭;小于3时,其分布较正态分布的峰平阔。因此边缘峰态的取值能反映出边缘的清晰（锐利）程度。
3  基于边缘峰态的清晰度评价算法
   本文算法的流程图如图2所示

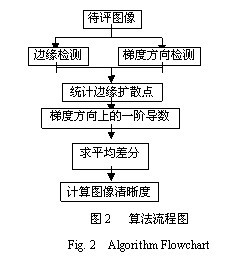
3.1边缘及梯度方向检测
      在实验中，我们采用了Sobel边缘检测算子。为了提高边缘的可靠性，减少噪声的影响，可以采用形态学算子滤除较小的孤立边缘点。
      梯度检测中我们使用高斯函数的一阶微分形式对图像进行滤波，得到

梯度方向为：

   由于数字图像以离散点阵的形式表示，我们将梯度方向均分为八个不同方向[2]，如图3中所示。

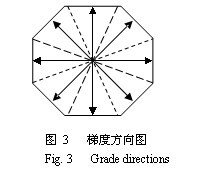
3.2 统计边缘扩散点，计算梯度方向的一阶导数
       对于每个边缘像素点，根据梯度方向的不同，我们沿梯度方向及其反方向上获取边缘扩散邻域，将得到的点集视为一个向量，计算该向量的一阶导数（在离散情况下即为差分）。为了尽量减少噪声和各种图像模式的影响，在得到各边缘扩散邻域的一阶导数后，我们还需要对其平均。值得注意的是，平均时只有相同位置的点才能相加。可以证明，梯度最大的地方就是实际的边缘点处，因此我们可以通过在边缘点附近获取边缘扩散邻域的局部最大梯度来实现。图4 是平均后图像的一阶导数脉冲图（扩散邻域取60个像素）。事实上，该图可近似认为图像的线扩展函数（LSF）分布。本文中，我们将根据尖峰的陡峭程度来衡量图像的模糊程度。

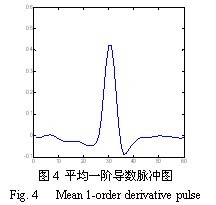
3.3计算图像清晰度
      前面我们提到，峰态信息能反映出分布曲线高峰的形态。因此，我们采用峰态信息作为模糊图像质量（清晰度）的度量。
　　　                     B=ln(K)　　　　　　　　（4）
       从以上讨论可以得知，边缘锐化程度越高，峰态值就越大，从而图像清晰度也越好。反之，峰态值越小，表明边缘越模糊，从而图像清晰度就越差。
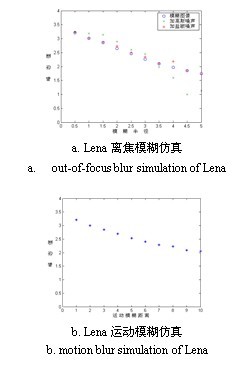
      首先我们用Lena图测试本文方法的有效性，对原图分别用半径为｛0.5 1 1.5 2 2.5 3 3.5 4 4.5 5｝的散焦函数进行模糊仿真，然后分别加以高斯白噪声（均值：0 方差：0.05）、盐椒噪声（噪声强度：0.01）以测试对噪声的鲁棒性，结果如Fig. 5(a)所示。可以看到，本文方法所得结果与模糊程度表现基本一致，且对噪声不是很敏感。
       为了测试不同模糊类型的影响，我们对Lena图进行运动模糊仿真（模糊距离：1 2 3 4 5 6 7 8 9 10，任取模糊方向，本处取）。从Fig. 5(b)中可以看出，在不知道模糊的先验知识的情况下，本方法也能得到较合理的结果。
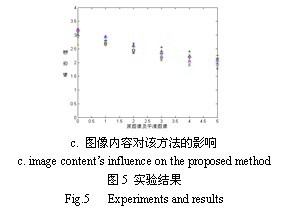
       最后，我们采用了LIVE的标准图像库[9]以测试不同图像内容对该方法的影响。我们任意选取了10幅标准图像（包括人脸、房屋、河流、道路等内容差异较大的图像），分别用高斯函数进行多次平滑，平滑次数越多，模糊程度越高。结果如图5(c)所示。

5  结　论
       针对模糊图像的边缘平滑特性，我们提出一种基于边缘峰态的无参考图像清晰度评价方法，先获取边缘扩散邻域的一阶微分，平均后对其求取峰态作为图像清晰度的度量，实验结果证实了该方法的有效性。目前存在的问题是，对高斯白噪声的模糊图像评价略有误差，可以先对图像平滑滤波处理以进一步提高对噪声的鲁棒性。

参 考 文 献

[1] P. Marziliano, F. Dufaux, S. Winkler, T. Ebrahimi, A no-reference perceptual blur metric [J]. Proceedings of the International Conference on Image Processing, Vol. 3, Rochester, NY, 2002, pp. 57–60
[2]　EePing Ong， Weisi Lin, Zhongkaiig Lu, Xiaokang Yang, Susir Yao, Feng Pan, Lijilrn Jiarrg, and Fulvio Moscheni， A no-reference quality metric for measuring image blur [J], 7th International Symposium on Signal Processing and Its Applications, Paris, France, July 1-4, 2003
[3] YC Chung, JM Wang, RR Bailey, SW Chen, and SL Chang, A Non-Parametric Blur Measure Based on Edge Analysis for Image Processing Applications [J], 2004 IEEE Conf. on CIS, Singapore, Dec 2004
[4]　Li q, Feng H J, Xu Z H, Bian M J, Shen S, Dai R C. Digital image sharpness evaluation function [J]. Acta Photonica Sinica, 2002, 31(6): 736~738[李奇，冯华君，徐之海，边美娟，申溯，戴瑞春. 数字图像清晰度评价函数研究[J]. 光子学报. 2002 ，31（6）：736～738]
[5]　Wang H N , Zhong W , Wang J , Xia D S. Research of Measurement for Digital Image Definition [J]. Journal of Image and Graphics, 2004, 9(7) [王鸿南，钟文，汪静，夏德深. 图像清晰度评价方法研究[J]. 中国图象图形学报. 2004，9（7）]
[6]　J. Caviedes, S. Gurbuz, No-reference sharpness metric based on local edge kurtosis[J], International Conference on Image Processing, vol. 3, pp. 53-56, Sep. 2002.
[7]　R. Ferzli, Lina J. Karam, J. Caviedes, A robust image sharpness metric based on kurtosis measurement of  wavelet coefficients [J], 1st International Workshop on Video Processing and Quality Metrics for Consumer Electronics
[8]　D. Li, RM Mersereau, S. Simske, Blur identification based on kurtosis minimization [J], Proc. IEEE ICIP. 2005. 3
[9]　H.R. Sheikh, Z. Wang, L. Cormack and A. C. Bovik, “LIVE image quality assessment database”, available at  
http://live.ece.utexas.edu/research/quality